mjleft.blogg.se - Peg solitaire game traingle

Peg solitaire game traingle code#
Peg solitaire game traingle download#

Int toIdx = GetIndex(ridx + 2, cidx + 2) We know that the column to the right always exists because it's a triangle! int fromIdx = GetIndex(ridx, cidx) Protected void AddDiagonalRightHop(Row r, int ridx, int cidx) Note that the column index stay constant. Protected void AddDiagonalLeftHop(Row r, int ridx, int cidx) Protected void AddHorizontalHop(Row r, int ridx, int cidx) Check for valid diagonal hop, which is any hop downward where the target cell exists. The idea here is to allow for diagonal down-left and down-right hops and left-to-right hops. Initializing all the possible hops populates the List allHops structure: It took me quite a while to realize that the Hop instance was being re-used for multiple iterations, thus overwriting the colors of a previous iteration! The issue of preserving color was actually the hardest bug to solve. The ToString() method gives us an easy way to display the solution in a ListBox of hops.However, because a hop preserves color state information, we need a cloned instance for the reason that the comment states.

In the board's model, there is only one instance of each possible hop. We'll see later that these colors are assigned when a hop is made based on the current game board state. A hop preserves the state of the peg colors involved in the hop.A hop knows its from, to, and cell hopped over indices.Ret = FromCellIndex.ToString() + " to " + ToCellIndex.ToString() + " over " + HoppedCellIndex.ToString() Hop hop = new Hop(FromCellIndex, ToCellIndex, HoppedCellIndex) / Hop instance's color state will be overwritten by the new hop. / Otherwise, the Hop instance might be re-used in a later iteration and the previous / /// We clone the Hop so that the color state is preserved for this *specific* hop. Public Hop( int from, int to, int hopped) More semantically friendly: public bool HasPeg I decided to borrow from Ruby to create an extension method that iterates on an integer with an optional starting offset: The algorithm only needs to determine which of these "hops" is legal for the current board configuration.

Peg solitaire game traingle download#

The Libs folder contains all the dependencies that FlowSharp uses, so you do not have to download and build that project.Ī lot of the work is done up front by setting up collections that have pre-determined all the possible "hops" from one "cell" to another.

If you want to play around with recursive yields, there's a YieldTest folder with a simple demo (shown later in the article.).

The actual demo app is found in the Demo folder.

The SLN file is found in the BrainTeaser folder.

Recursive with callback - again the search stack is an artifact of recursion.

Recursive using yield - the search stack is an artifact of recursion.

Iterative - the search stack is handled as handled as an actual Stack object.

Implements three different algorithms so you can peruse the pros and cons of each:.

As with the actual cheap game, there are 3 different colored pegs - yellow, blue, and red - which the UI implements, randomly assigned when you start the demo.

Let's you single step through the solution and watch each step so you can memorize the solution and impress your friends!.

Embeds FlowSharp so you can watch the algorithm go through the process of finding a solution (why re-invent the wheel?).

Peg solitaire game traingle code#

Has a funky extension method which may or may not make the code more readable.

implemented iteration and recursion alternatives.Īnd as is apt to occur, I went way overboard.

had a snazzy UI so you could watch the algorithm processing.

And more to the point, none of the algorithms presented: And of course, one can challenge oneself to write the code as elegantly and efficiently as possible, etc. OK, so while there are several solutions, I actually didn't find one in C#, and even if I had, there is a certain pleasure in writing something like this oneself, even if it's been done before.

There's a C program here that solves the puzzle.

There is a Java article here on CodeProject.

Watching one of my coworkers futility go through various failed iterations, I had the obvious thought - write a program to find solutions to the puzzle! The second obvious thought was, someone must have done this! Well, turns out, not really.

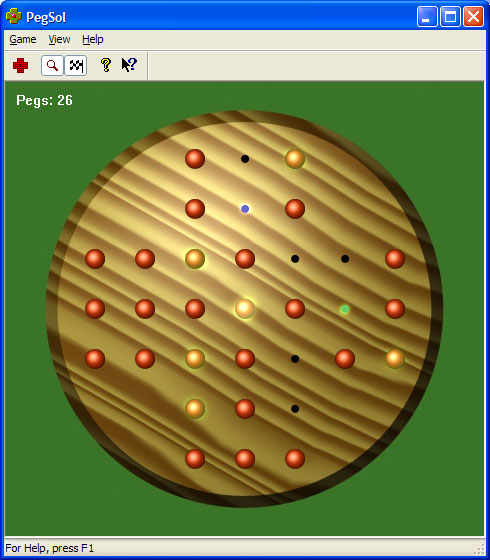
The goal is to remain with just one peg left.įor a roomful of programmers, no one (including me!) so far has been able to solve the puzzle. We've probably all played them - the idea being you start with one empty hole, the rest are filled with pegs, and each move consists of hopping a peg to an empty location, thus removing the peg you just hopped. We have these brain teaser puzzles at work: Step 1: Initializing the FlowSharp modules with the bootstrap loader.Why No Marshalling Onto The Main Thread?.The Recursive Step and Continue Algorithm.What about a Step-And-Continue callback?.